Errores en altimetría; error de esfericidad y error de refracción

Los errores en altimetría son dos errores de lo más común como son el error de esfericidad y el error de refracción. El primero de ellos se debe a la esfericidad de la Tierra, algo con lo que todo el mundo cuenta, pero que hay que solucionar para conseguir unas medidas lo más precisas y fiables posibles. El Segundo se debe de la refracción atmosférica, y aunque no resulta tan evidente como el  error de esfericidad hay que corregirlo igualmente.

Errores en altimetría

A continuación os mostramos con detalle ambos errores y como trabajar con ellos en cualquier proyecto topográfico.

Error de esfericidad

Este error se debe a la forma esférica que tiene la Tierra y con la que debemos de convivir en cualquier tipo de trabajo. En visuales inferiores en longitud de arco a 5' o lo que es lo mismo 10 kilómetros se consideran iguales el arco, la cuerda y la tangente.

Teniendo en cuenta esto, el error de esfericidad sería;

D^2 + R^2 = (R+ εe)^2

D^2 + R^2 = R^2 + εe^2 + 2R εe

εe^2 ≈ 0, podemos despreciar su cuadrado ya que se trata de una magnitud realmente pequeña dentro de la topografía

D = Distancia reducida

εe= D^2/(2R) 

Este error será siempre positivo (en el caso de no ser así es que estás calculándolo de forma incorrecta), y en todos los casos de signo positivo y se debe de sumar al desnivel que hayamos calculado.

Error de refracción

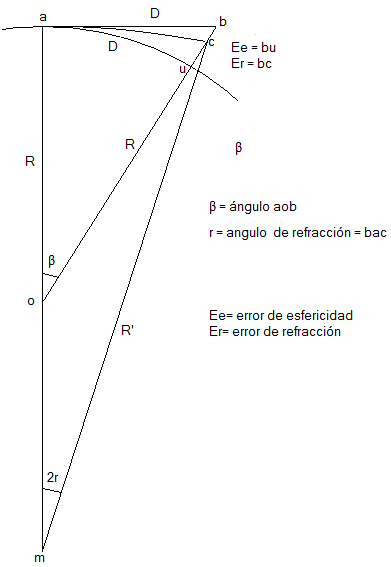
Este error se debe a la refracción atmosférica, siendo una consecuencia de la variación de la densidad del aire por donde atraviesa la visual. La densidad del aire, por normal general, es mayor cuanto más cerca se encuentra de la superficie, con esto podemos concluir que la visual se refracta de tal forma que se acercará al terreno, tal y como se muestra en el siguiente esquema;

Este error tiene siempre signo negativo (si no es así, es que estás realizando alguno de los cálculos de forma incorrecta) y se compensa de forma parcial con el error de esfericidad.

Por desgracia la densidad del aire no siempre la premisa de ir de mayor a menor cuando nos acercamos al terreno, ya que dependerá en gran medida de la zona donde nos encontremos trabajando. Si te encuentras con esto y por ejemplo estás trabajando en una zona muy cálida, puede que la densidad del aire cambie, y por tanto no tendrá aplicación el error tal y como te lo mostramos en este artículo, y deberás de buscar otras fórmulas diferentes para calcularlo.

En este caso la visual desde el punto "a" no iría al punto "b" sino que debería de ir a "c" y entonces el error de refracción sería εr, que a su vez es igual a la distancia bc.

Se llama ángulo de refracción a r=bac

• mab = 100g
• mac = 100g – r
• mac = mca = 100g – r
• mac + mca + amb = 200 g
• 100 g – r + 100 g – r + amb = 200 g
• Luego: amb = 2r

Ahora si nos centramos en el triángulo rectángulo amb tendremos que;

R’2 + D2 = (R’ + εr)2 = R’2 + εr 2 + 2R’ εr = R’2 + 2R’ εr

Suponemos despreciable εr 2

D^2 = 2R' εr

εr = D^2/2R'

Ahora si nos fijamos en el dibujo que se muestra a continuación, y teniendo en cuenta lo que ya mencionamos anteriormente, de que para ángulos menores de 5', el arco, la cuerda t la tangente son iguales a D, vamos a tener;

• β = D/R
• 2r = D/R’

Luego:

• 2rR’ = βR
• R/R’ = 2r/β = 2K

Donde K es el coeficiente de refracción y que podremos calcular de una forma experimental de la siguiente forma;

R’ = R/2K

Y ahora si sustituimos en Sustituyendo en εr = D^2/2R' tendremos: εr = D^2K/R

Considerando ambos errores tendremos:

εt=εe+εr=D2/2R-D2K/R=D2/R(0.5-K)

εt=D2/R(0.5-K)

En España se considera que el valor medio de k es igual a 0,08 por lo que tendríamos que;

εt=0.42 *D2/R

Ahora si introducimos el dato conocido del radio de la Tierra, que es R=6370 kilómetros y que D es la distancia horizontal o reducida, tendremos que para las siguientes distancias , el error de refracción será;

• D= 100 metros - Error de refracción=0,66
• D= 200 metros - Error de refracción=2,6
• D= 300 metros - Error de refracción=5,9
• D= 500 metros - Error de refracción=16,5
• D= 1000 metros - Error de refracción=66,0
• D= 2000 metros - Error de refracción=264,0

Podemos afirmar, sin temor a equivocarnos, que el error aumenta con el cuadrado de la distancia, con lo que si trabajamos con visuales largas debemos de tener en cuenta y muy presente en todo momento.

¿Has comprendido la importancia y necesidad de tener en cuenta tanto el error de esfericidad como el error de refracción o lo que es lo mismo, los errores en altimetría?